前言
好久没写过东西了哈哈,有些时候当你会得越多、学习得越多、或者接触的牛人多了,就会发现知道原来自己很渺小,自己懂得很少,有些东西真的需要各种天赋,尤其是数学天赋。比如:图形学、
继续阅读
好久没写过东西了哈哈,有些时候当你会得越多、学习得越多、或者接触的牛人多了,就会发现知道原来自己很渺小,自己懂得很少,有些东西真的需要各种天赋,尤其是数学天赋。比如:图形学、
继续阅读
最近在使用 three.js 移植一个 shader 效果时遇到一个问题,报错如下:
THREE.WebGLProgram: shader error: 0 35715 false gl.getProgramInfoLog No compiled fragment shader when at least one graphics shader is attached.
THREE.WebGLShader: gl.getShaderInfoLog() fragment
ERROR: 0:23: 'dFdx' : no matching overloaded function found
ERROR: 0:23: 'dFdy' : no matching overloaded function found
ERROR: 0:23: 'cross' : no matching overloaded function found
WARNING: 0:? : 'normalize' : operation result is undefined for the values passed in
ERROR: 0:23: '=' : dimension mismatch
ERROR: 0:23: '=' : cannot convert from 'const mediump float' to 'highp 3-component vector of float'
本次使用的 three.js 的版本如下:
"three": "^0.122.0",
百度了很多解决方案 继续阅读
水gis 用 cesium ,bim 或建筑单纯展示和运维管理用 three
osgb 可以采用 3dtiles
远近变的是 lod + mipmap
航拍点云 点云转模型用 pcl
Meshlab 把点云文件转换为网格模型
cesuim 加载倾斜摄影 OSGB 三维数据
Blensor: Blender Sensor Simulation 这是基于 Blender 的一个插件。和直接提取点云数据的方法不同,Blensor 是将三维模型导入 Blender 中然后模拟使用 Scanner 对三维模型进行扫描。这样做的好处是和实际扫出来的数据很像,可以方便地选择扫描的位置、设置多个点云用于registration、添加 noise 或者模拟的设备。这些特性在需要 toy data 进行测试时比较有用 继续阅读
顶点连接顺序(Winding order)
默认情况下,逆时针的顶点连接顺序被定义为三角形的正面。
当定义你的顶点顺序时,你如果定义能够看到的一个三角形,那它一定是正面朝向的,所以你定义的三角形应该是逆时针的,就像你直接面向这个三角形。把所有的顶点指定成这样是件炫酷的事,实际的顶点连接顺序是在光栅化阶段(Rasterization stage)计算的,所以当顶点着色器已经运行后。顶点就能够在观察者的观察点被 继续阅读
为什么自定义的纹理没有显示出来?这是因为 WebGL 对纹理有一种严格的限制,在两个维度上都不是 2 的幂。2 的幂是1,2,4,8,16,32,64,128,256,512,1024,2048,等等。假如 3D 物体的面长宽是 256 x 256。256 是 2 的幂,而自定义的纹理图的长宽为 320 x 240。这两个都不是2的幂,因此尝试显示纹理时会显示失败。在着色器中,当调用 texture2D 并且引用的纹理设置不正确时,WebGL 将使用黑色的颜色(0,0,0,1)代替 继续阅读
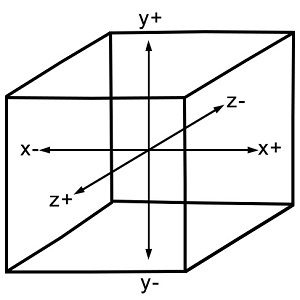
坐标系统 Coordinate System
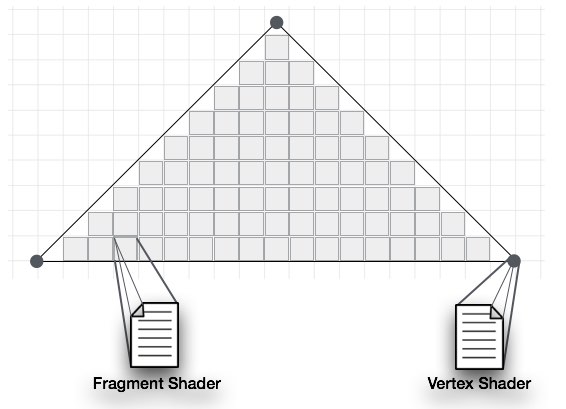
顶点 / 片元(片段)着色器 Vertex Shader / Fragment Shader(Pixel Shader)
球坐标系的基向量
r, 就是向量的本身的长度, 也就是, r = 根号(x^2 + y^2 + z^2), r 的方向是 radial direction, 就是本身那个向量的方向。
phi 和 theta 是两个角度.物理书中,一般习惯是,
theta 是向量和 z 轴的夹角。phi 是向量在 xy 平面上的投影和 x 轴的夹角 继续阅读