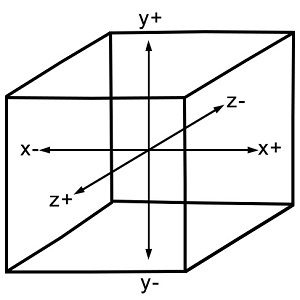
坐标系统 Coordinate System
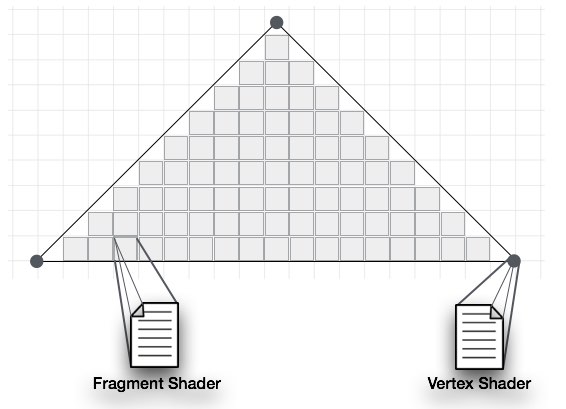
顶点 / 片元(片段)着色器 Vertex Shader / Fragment Shader(Pixel Shader)
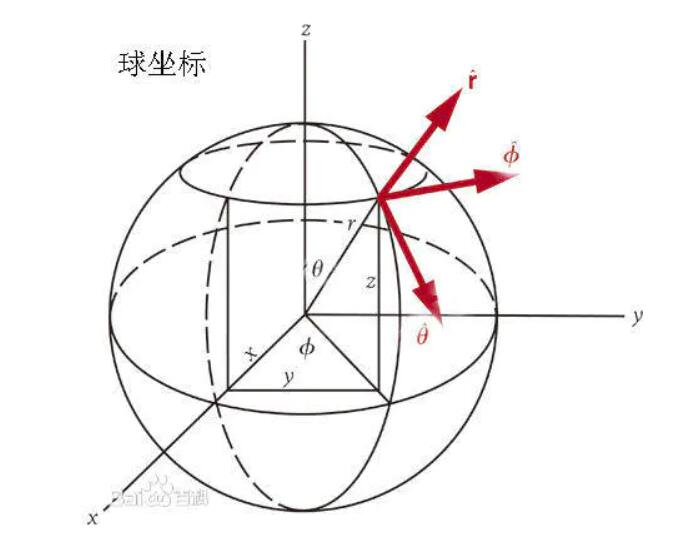
球坐标系的基向量
r, 就是向量的本身的长度, 也就是, r = 根号(x^2 + y^2 + z^2), r 的方向是 radial direction, 就是本身那个向量的方向。
phi 和 theta 是两个角度.物理书中,一般习惯是,
theta 是向量和 z 轴的夹角。phi 是向量在 xy 平面上的投影和 x 轴的夹角。
z = r * cos(theta)
xy 平面上那个投影的长度 = r * sin(theta)
所以, x = r * sin(theta) * cos(phi)
y = r * sin(theta) * sin(phi).
theta 和 phi 也是有方向的.他们的方向不是那么重要.是逆时针走的话是他们增加的方向(正方向)。
Fov / fieldOfViewRadians
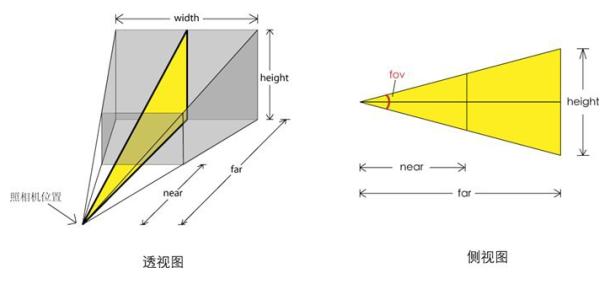
视场;视场角;视野;视角;视场角度
fovy 的值越小,近裁剪面越小,同样大小的模型就显得大;
反之,fovy 的值越大,近裁剪面越大,同样大小的模型就显得小;
虽然模型并不是在近裁剪面绘制的,是在近裁剪面和远裁剪面的中间,视椎体内。
// Compute the projection matrix
var aspect = gl.canvas.clientWidth / gl.canvas.clientHeight;
var zNear = 1;
var zFar = 2000;
var projectionMatrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar);
参考引用:https://blog.csdn.net/a117653909/article/details/7765621
归一化 Normalize
归一化也就是一个做一个类似 1.0 的矢量,如果是二维旋转时, 那就是的单位圆在二维旋转中用法,在三维中需要一个单位球,单位向量表示单位球上的点。
function normalize(v) {
var length = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
// make sure we don't divide by 0.
if (length > 0.00001) {
return [v[0] / length, v[1] / length, v[2] / length];
} else {
return [0, 0, 0];
}
}
透视投影矩阵 Perspective
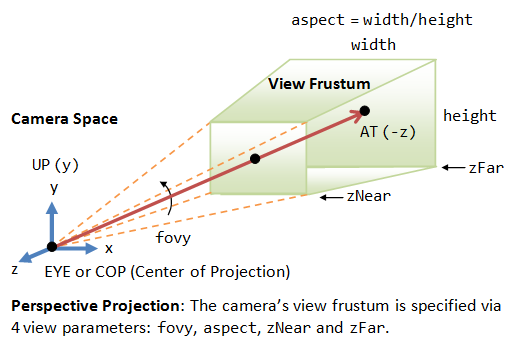
mat4 的 perspective 函数。该函数通过 y 方向上可见区域的夹角(称 Fov 或 Fovy)、纵横比(aspect)、和近(zNear)远(zFar)距离计算透视投影矩阵 Perspective Projection Matrix(常用 MVP 中的 P)
function perspective(out, fovy, aspect, near, far)
参考引用:https://github.com/toji/gl-matrix/blob/master/src/mat4.js
视图矩阵 View Matrix
大多数三维数学库都有 lookAt 方法,通常它是用于计算 “视图矩阵” 而不是 “相机矩阵”。
视图矩阵使用 mat4.lookAt 函数计算。该函数的后三个参数是三个 vec3 类型,分别表示眼睛的位置、场景中心的位置和从观察者的角度往上的向量;第一个参数用来保存计算好的矩阵
function lookAt(out, eye, center, up)
参考引用:https://github.com/toji/gl-matrix/blob/master/src/mat4.js
另一种计算方法(不常用):

视图矩阵是将所有物体以相反于相机的方向运动, 尽管相机还是在原点但是相对关系是可预知的。我们可以使用 inverse 方法计算逆矩阵( 完全对立的转换矩阵),在这个例子中提供的是绕原点转动的矩阵, 它的逆矩阵是移动相机以外的所有物体,好像相机在原点一样。
var numFs = 5; var radius = 200; // 计算相机的矩阵 var cameraMatrix = m4.yRotation(cameraAngleRadians); cameraMatrix = m4.translate(cameraMatrix, 0, 0, radius * 1.5); // 通过相机矩阵计算视图矩阵 var viewMatrix = m4.inverse(cameraMatrix);
参考引用:https://webglfundamentals.org/webgl/lessons/zh_cn/webgl-3d-camera.html
还有另一种计算方法,lookAt 的另外的版本,用于计算 “相机矩阵”,再求逆得到 “视图矩阵”(不常用):
// 计算第一个 F 的位置
var fPosition = [radius, 0, 0];
// 计算相机在圆上的位置矩阵
var cameraMatrix = m4.yRotation(cameraAngleRadians);
cameraMatrix = m4.translate(cameraMatrix, 0, 0, radius * 1.5);
// 获得矩阵中相机的位置
var cameraPosition = [
cameraMatrix[12],
cameraMatrix[13],
cameraMatrix[14],
];
var up = [0, 1, 0];
// 计算相机的朝向矩阵
var cameraMatrix = m4.lookAt(cameraPosition, fPosition, up);
// 通过相机矩阵获得视图矩阵
var viewMatrix = m4.inverse(cameraMatrix);
// 计算叉乘的代码
function cross(a, b) {
return [a[1] * b[2] - a[2] * b[1],
a[2] * b[0] - a[0] * b[2],
a[0] * b[1] - a[1] * b[0]];
}
// 向量相减的代码
function subtractVectors(a, b) {
return [a[0] - b[0], a[1] - b[1], a[2] - b[2]];
}
// 归一化向量的代码
function normalize(v) {
var length = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
// 确定不会除以 0
if (length > 0.00001) {
return [v[0] / length, v[1] / length, v[2] / length];
} else {
return [0, 0, 0];
}
}
// 计算 “朝向” 矩阵的代码
var m4 = {
lookAt: function(cameraPosition, target, up) {
var zAxis = normalize(
subtractVectors(cameraPosition, target));
var xAxis = normalize(cross(up, zAxis));
var yAxis = normalize(cross(zAxis, xAxis));
return [
xAxis[0], xAxis[1], xAxis[2], 0,
yAxis[0], yAxis[1], yAxis[2], 0,
zAxis[0], zAxis[1], zAxis[2], 0,
cameraPosition[0],
cameraPosition[1],
cameraPosition[2],
1,
];
}
}
参考引用:https://webglfundamentals.org/webgl/lessons/zh_cn/webgl-3d-camera.html
正交投影 / 正射投影 Orthogonal Projection
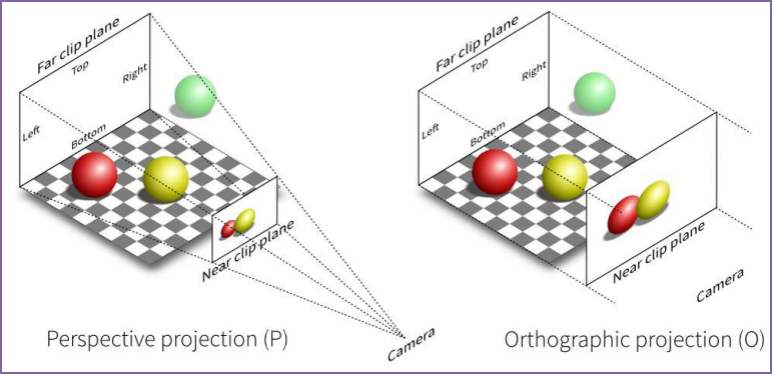
正交投影就是用一束平行光去照射物体所投影,这个过程就是正交投影
function ortho(out, left, right, bottom, top, near, far)
Quaternions(四元数)
四元数可以表示出以[ 任意方向的轴 ]进行[ 任意角度的旋转 ]。
构成四元数的元素,就是一个拥有三个元素的向量和一个角度。这就是四元数了。
四元数一般来说,像下面这样表示。
Q = (t; x, y, z)
上面的 t 叫做实数部分,向量部分的三个元素叫做虚数部分
用四元数来旋转
// 以原点为中心的轴向量 = (x, y, z) // 旋转角度 = th Q = (cos(th / 2); x * sin(th / 2), y * sin(th / 2), z * sin(th / 2)) // Q 的共轭四元数 R 。共轭四元数只是将四元数的X ・ Y ・ Z 的值取反 R = (cos(th / 2); -x * sin(th / 2), -y * sin(th / 2), -z * sin(th / 2))
参考引用:https://blog.csdn.net/lufy_legend/article/details/77496015
THREE.Euler() 欧拉角
用法 THREE.Euler( a , b , c , ‘xyz’ );
表示将一个几何体绕 x 轴旋转 a 度,绕 y 轴旋转 b 度,绕z轴旋转 c 度;并且旋转的顺序是 xyz ; 第三个参数旋转顺序可以是 ’XYZ’, ‘YZX’, ‘ZXY’, ‘XZY’, ‘YXZ’, ‘ZYX’
参考引用:https://blog.csdn.net/kingov/article/details/77888289
GLSL (OpenGL 着色语言 OpenGL Shading Language)
语法跟 C 语言很类似,在可编程管线中我们必须要纯手写顶点和片源着色器,这里就要求必须使用 GLSL,自行编译,链接,使用
参考引用:https://www.jianshu.com/p/66b10062bd67
向心的 centripetal
弦的 chordal
投射阴影 castShadow
射线 Raycaster
three.js 利用射线 Raycaster 进行碰撞检测(https://www.jb51.net/article/182528.htm)
在 three.js,可以利用 THREE.Raycaster 来达到点击与交互,即选择物体的操作(https://blog.csdn.net/flame_007/article/details/88726098)
WEBGL 之 attribute,uniform,varying
1. attibute 变量的获取与传值
attribute 为存储限定符,表示接下来的变量是一个 attribute 变量,数据将从着色器外部传递给变量,必须是全局的,只有顶点着色器可以使用,传输与顶点相关的数据。attribute 的类型只能为 float,vec2,vec3,vec4,mat2,mat3,mat4
var vshader=
'attribute vec4 a_Position;\n'+
'void main(){\n'+
'gl_position=a_Position;\n'+
'gl_Pointsize=10.0;\n'+
'}\n';
// 第一个参数为程序对象
var a_position = gl.getAttribLocation(gl.program, 'a_Position');
// 本来是 vec4,第四个自动补齐
gl.vertexAttrib3f(a_position, 0.0, 0.0, 0.0);
其他函数
gl.vertex1f(location,v0);
gl.vertex2f(location,v0,.v1);
gl.vertex3f(location,v0,v1,v2);
gl.vertex4f(location,v0,v1,v2,v3);
2. uniform 变量的获取与传值
uniform 变量可以在顶点着色器与片元着色器中,且必须是全局的。与顶点无关,对所有顶点相同如变换矩阵。如果在顶点与片源着色器中使用了同名的 uniform 变量,那么就会被两种着色器共享。
var FRAGMENT_SHADER=
'precision mediump float;\n'+
'uniform vec4 u_FragColor;\n'+
'void main(){\n'+
'gl_FragColor=u_FragColor;\n'+
'}'
var u_FragColor = gl.getUniformLocation(gl.program, 'u_FragColor');
gl.uniform4f(u_FragColor, 0.0, 1.0, 1.0, 1.0);
3. varying 变量
varying 同时在顶点着色器和片元着色器中定义,用于在两者之间传递数据。
var vertexShaderSrc = `
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
void main(){
gl_Position = a_Position;
v_Color = a_Color;
}`;
var fragmentShaderSrc = `
precision mediump float; // float变量没有默认精度,所以使用前必须声明,否则会出错
varying vec4 v_Color;
void main(){
gl_FragColor = v_Color;
}`;
参考引用:
https://www.jianshu.com/p/11b91d95fe0d
https://blog.csdn.net/xufeng0991/article/details/75675619
Sphere 球; 球体;
geometry 几何形状; 几何图形; 几何结构;
resolution 屏幕分辨率
齐次坐标 Homogeneous Coordinates
在欧几里得(或称笛卡尔)空间里描述2D/3D 几何物体是很理想的,但在投影空间里面却并不见得。 我们用 (x, y) 表示笛卡尔空间中的一个 2D 点,而处于无限远处的点 (∞,∞) 在笛卡尔空间里是没有意义的。投影空间里的两条平行线会在无限远处相交于一点,但笛卡尔空间里面无法搞定这个问题(因为无限远处的点在笛卡尔空间里是没有意义的),因此数学家想出齐次坐标这个点子来了。
参考引用:https://www.cnblogs.com/zhizhan/p/3999885.html
向量点乘(Dot Product)和向量叉乘(Cross Product)

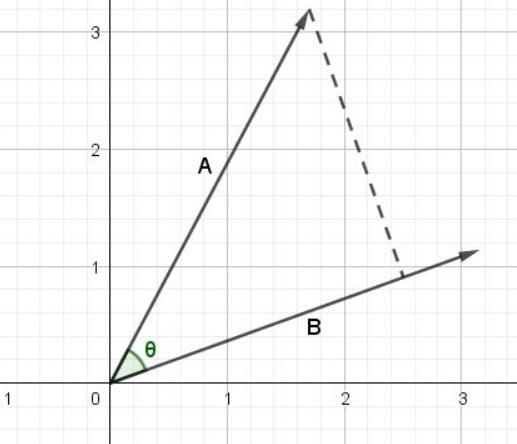
两个向量点乘,点乘的结果是一个标量。数值计算的结果就代表几何上的投影,应用:1计算长度和角度2检测正交性3 求三角形面积
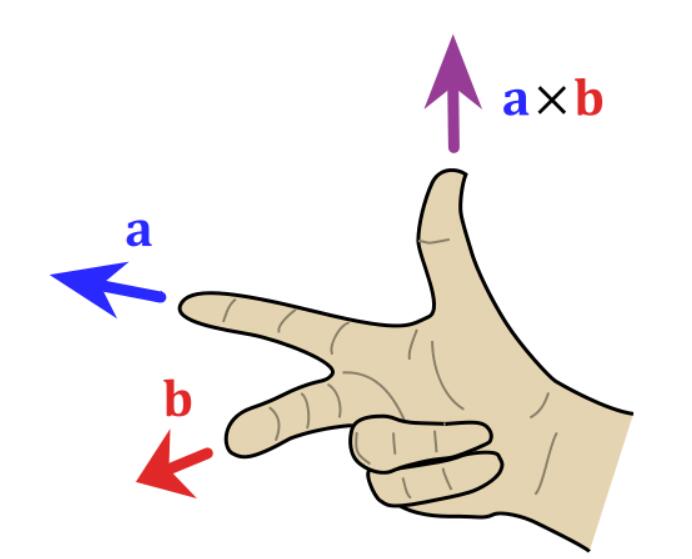
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。在三维几何中,向量 a 和向量 b 的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。在 3D 图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于 a,b 的法向量,从而构建X、Y、Z坐标系。如下图所示:
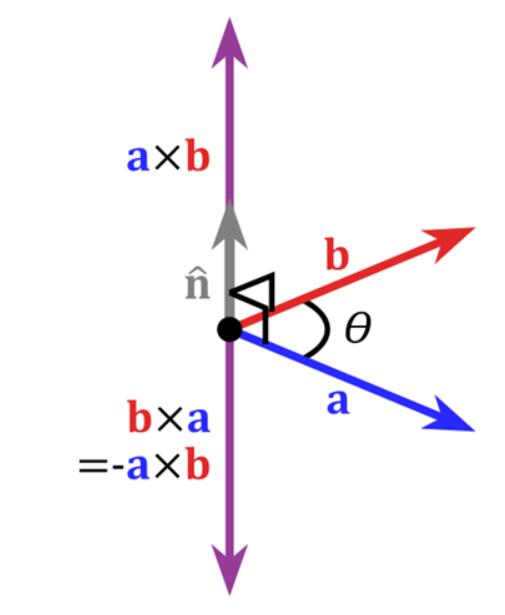
在二维空间中,叉乘还有另外一个几何意义就是:aXb等于由向量a和向量b构成的平行四边形的面积。
参考引用:
https://www.zhihu.com/question/21080171
https://blog.csdn.net/dcrmg/article/details/52416832
逆矩阵(inverse matrix)
点 p,矩阵 m,
p' = p * m;
p = p' * m~;
或者
p * M = p'
假设 M 的逆是 T
那么 p' * T = p
这种一般用来反推位置之类的
参考引用:
https://bbs.csdn.net/topics/360119530
https://blog.csdn.net/vernice/article/details/48506027
转置矩阵(Transpose)
在二维空间里矩阵的 转置 ,就相当于 得到关于某个点对称的二维图像,有点像A4纸上写着矩阵的数表,摁着它的右上角,揭着它的左下角沿对角线往上掀啦
在三维空间里矩阵的 转置 ,同样是相当于 得到关于某个点对称的三维立体,想象一下一个正方体关于某个点对称的情形,这是一种特殊的旋转,左乘一个矩阵也可以殊途同归达到转置的效果
一个向量乘以另一个向量的转置,这是内积运算。内积运算从几何角度上说,是一个投影。内积运算从几何角度上说,是一个投影。举一个例子,例如有一颗树,当太阳在树的正上方的时候,树的影子只有一个点,也就是说树在大地的投影为 0,这里可以把大树抽象为一个向量,大地是一个平面,太阳光下的影子就是一个投影操作。投影为 0 说明内积为 0,内积为 0 说明二者是正交(垂直)关系,因为大树垂直于大地这个平面。如果大树倒塌了,那么大树在地面的投影等于它本身(这就可以类比向量到自身的投影,或者说自己跟自己的内积)。正是这个投影运算,我们可以定义两个向量的夹角 α, cosα = (a,b) / |a||b|, 这其实就是平面三角形余弦定理到高维空间的推广。正交(垂直)就是夹角为 π/2, 等价于内积为 0。
Photoshop 中的 Ctrl+T,T 就是 Transpose(转置矩阵)的缩写。
参考引用:
https://www.zhihu.com/question/38372986?rf=34597377
https://www.zhihu.com/question/40049682/answer/608794353
法向量(Normal Vector)
在三维图形学中法向量就是描述面的朝向的单位向量
法向量,是空间解析几何的一个概念,垂直于平面的直线所表示的向量为该平面的法向量。法向量适用于解析几何。由于空间内有无数个直线垂直于已知平面,因此一个平面都存在无数个法向量(包括两个单位法向量)。
还可参考:
https://blog.csdn.net/liyaxin2010/article/details/84761280
高光亮度 (specular) 和光泽度 (gloss) 漫反射光亮度(Diffuse Shading)
不同的光照系统里 specular 和 gloss 代表的含义不同。最简单的理解,gloss 是光泽度,也叫表面粗糙度,代表物体表面状态。specular 是高光亮度。上时代游戏光照模型里 gloss 和 specular 从感官上可以表达材质。PBR 光照系统里 specular 和 diffuse 一起决定物体表面材质,gloss 是表面粗糙度,和材质没有绝对关系。
漫反射,是投射在粗糙表面上的光向各个方向反射的现象。当一束平行的入射光线射到粗糙的表面时,表面会把光线向着四面八方反射,所以入射线虽然互相平行,由于各点的法线方向不一致,造成反射光线向不同的方向无规则地反射,这种反射称之为“漫反射”或“漫射”。这种反射的光称为漫射光。很多物体,如植物、墙壁、衣服等,其表面粗看起来似乎是平滑,但用放大镜仔细观察,就会看到其表面是凹凸不平的,所以本来是平行的太阳光被这些表面反射后,弥漫地射向不同方向。
可参考:
https://edwardzhong.github.io/2019/04/29/webgltexture/
球坐标系构建球模型
设定球的半径为单位1,则
x = sinθ.sinφ
y = cosθ
z = sinθ.cosφ
θ[0,π]
φ[-π,π]
两种构建方式
https://webglfundamentals.org/webgl/webgl-text-texture-different-colors.html
https://www.jianshu.com/p/9d2a5f1ec00f